この記事でわかること
- Fourier Neural Operatorをどのように動かせばいいかわかる
- Fourier Neural Operatorの適用条件を理解できる
対象読者
- 機械学習による物理シミュレーションの高速化に取り組んでいる人・興味がある人
- CAE従事者で、計算時間や解析の設定難易度に課題を感じている人
- Fourier Neural Operator によってCAE解析を高速化したい人
- 細かいことはいいから、入出力と適用範囲・動かし方を知りたい人
はじめに
この記事では、PhysicsNeMoのモデルの一つであるFourier Neural Operatorのサンプルコードを実行してみる。
Fourier Neural Operator の手法概要についてはこちらの記事を確認してほしい。
今回実装したコードは、こちらを参考にしてほしい。
Fourier Neural Operator を利用するにはどのようなデータを用意すれば良いかを理解すること
コード実行には以下の点に注意してほしい。
- PhysicsNeMoライブラリが必要
- GPUメモリが12GB程度必要
サンプルコードの実行
環境構築
まず、Fourier Neural Operator のサンプルコードを取得しよう。
PhysicsNeMoの公式gitにexamplesがあるので、fnoのサンプルコードをダウンロードしておく。
必要なパッケージをinstall しておく。
pip install -r requirements.txtこれで準備は完了である。
学習の実行
それでは、Fourier Neural Operator の 学習を実行してみよう
サンプルコードでは、2次元Darcy流れに関する学習が実装されている。問題設定やデータ構造は後程説明しよう。
このサンプルコードではデータ生成も、train関数に含まれているので、実行はとても簡単である。
python train_fno_darcy.py 下記のようなログがターミナルに現れれば、実行完了。
Warp 1.8.1 initialized:
CUDA Toolkit 12.8, Driver 12.9
Devices:
"cpu" : "x86_64"
"cuda:0" : "NVIDIA GeForce RTX 5070" (12 GiB, sm_120, mempool enabled)
Kernel cache:
/home/user/.cache/warp/1.8.1
[2025-09-07 10:50:56,809][checkpoint][WARNING] - Provided checkpoint directory ./checkpoints does not exist, skipping load
[2025-09-07 10:50:56,810][darcy_fno][WARNING] - Model FourierNeuralOperator does not support AMP on GPUs, turning off
[2025-09-07 10:50:56,828][darcy_fno][WARNING] - Model FourierNeuralOperator does not support AMP on GPUs, turning off
[2025-09-07 10:50:56,829][darcy_fno][INFO] - Training started...
[2025-09-07 10:52:50,413][train][INFO] - Epoch 1 Metrics: Learning Rate = 1.000e-03, loss = 7.756e-01
[2025-09-07 10:52:50,415][train][INFO] - Epoch Execution Time: 1.139e+02s, Time/Iter: 3.559e+03ms学習が進むと、定期的に検証が実行され、検証結果が図1のように表示される。
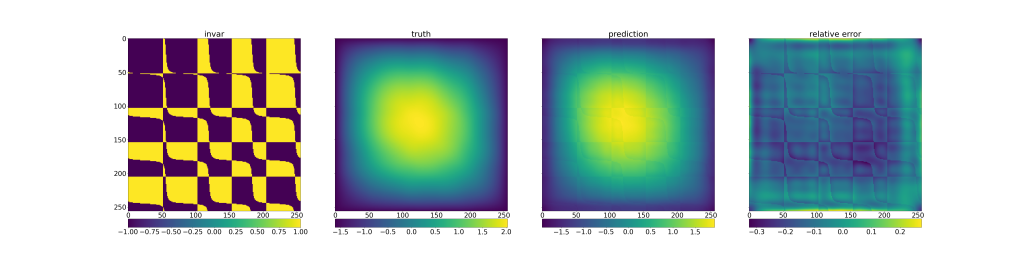
Fourier Neural operatorのvalidationが出力する図
図1の見方は、後ほど説明する。
また、定期的に学習パラメーターがcheckpointsというフォルダーに保存される。.ptというファイルには、学習パラメーターだけでなく、最適化に関する情報も保存される。.mdlusはPhysicsNeMo固有のファイル形式で、学習パラメーターとモデル名などのメタ情報が含まれている。
学習が進み、指定の回数だけイテレーションが進んだら、学習が終了する。
データセット 解説
この章では、FNOのサンプルコードが扱っているデータセットについて解説をし、FNOを利用するためにどの様なデータを用意すれば良いか理解する。
問題設定
まずはサンプルコードにおける問題設定を説明する。
サンプルコードでは、下記の2次元Darcy流れを扱っている。
\begin{equation} \begin{aligned}-\nabla \cdot (a(x)\nabla u(x)) &= f(x)\qquad x\in (0, 1)^2 \\u(x) &= 0 \qquad x\in \partial (0, 1)^2\end{aligned}\label{darcy}\end{equation}
サンプルコードの問題設定は、
拡散係数 $a(x)$ を入力に、式(1)の解 $u(x)$ を出力にするような問題を設定している。( $f(x) = 1$ と固定されている。) つまり、次のような学習可能作用素 $FNO$ を求めることが目的である。
\begin{equation} FNO(a) = u \end{equation}
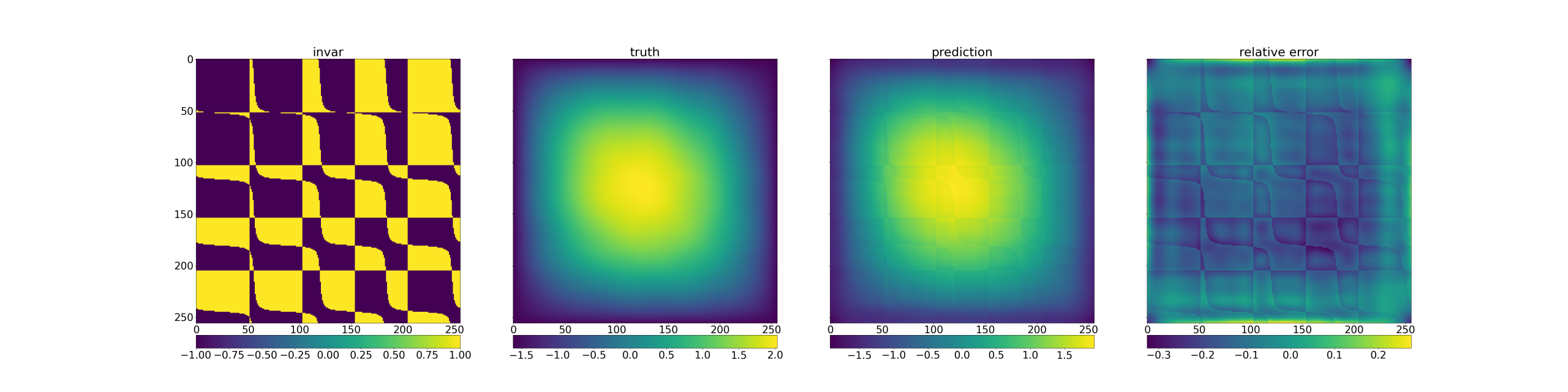
図1を見ると、一番左の図が入力の $a(x)$ 左から2番目の図が正解となる $u(x)$ 左から3番目の図が予測した $u(x)$ 一番右の図が 正解と予測結果の誤差を表している。
他の問題設定の例として、非定常の問題を考えよう。
非定常なら、前の時刻 $u(t-1, x)$ を入力に、次の時刻 $u(t, x)$ を出力し、時間方向はRNNのように計算をするという設定も考えられる。
あるいは、初期値 $u(0, x)$ を入力に時空間の関数 $u(t, x)$ を出力するということも考えられる。実装の都合上、解像度の次元数は合わせないといけないので、入力は時間方向に複製する処理が必要である。
上記のような関数を入力にできることがFourier Neural Networkの強みである。ここで、$f(x)$ を固定としたが、もちろん $ \alpha(x) = (a(x), f(x))$ として、$ \alpha(x) $ を入力にすることもできる。
データセットについて
入出力のデータ構造
前述したとおり、サンプルコードでは、$a(x)$ を入力にして、$u(x)$ を出力するような機械学習タスクである。
ここで、Fourier Neural Network の制約として、入出力の関数を格子点で離散化する必要がある。
そのため、$a(x), u(x)$ は、$a_{ij}\in \mathbb{R}, u_{ij} \in \mathbb{R}, (1\leq i \leq H, 1\leq j \leq W)$ とテンソル形式で離散化する必要がある。この時、点 $(i+1, j+1)$ は点 $(i, j)$ に対し、$\frac{1}{H}, \frac{1}{W}$だけ進んだ座標である必要がある。
ただし、サンプル間で解像度は等しい必要はない。(各index が 座標に変換できれば良い。この点がCNNベース手法とは異なる点である。)
データ構造に関して補足が2つある。
- 厳密には、Fourier Neural Network は構造格子でなくてもモデルを構築できる(別記事参照)。一方、その場合他手法に比べて計算が遅くなる。PhysicsNeMoの実装では、構造格子を前提としているようだ。
- 実際の学習の時はバッチ処理をすることがある。その時は解像度を合わせないとテンソル演算ができないので、解像度が一番大きいテンソルに合わせて、足りない要素を0埋めする必要がある。
データ生成について
よくある機械学習のタスクでは、予めデータを生成しておいて訓練データを何度も使って、学習させることが多い。
一方、式(\ref{darcy})はかなり高速に解くことができるので、
$a$ を生成 → 式(\ref{darcy})で、学習データ $ (a, u)$を生成→ $\tilde{u}=FNO(a)$で予測→ $u, \tilde{u}$ で誤差を計算 → 学習パラメーター更新 → $a$ を生成→・・・
という流れになっている。
ここで、$a$ は周波数空間で乱数を使って生成している。(そのため図1の $a$ では周期的な構造となっている)
本来のFourie Neural Operator の役割は、解くのに時間がかかる数値計算を高速化することであるから、今回のように簡単にデータ生成が出来ないことも多い。また、Fourie Neural Operatorの場合、構造化したデータが必要であるから、実際の数値計算結果をテンソルデータに変換することも必要である。その観点から、データをどのように生成するかは非常に大きな問題である。
コード解説
この章では、サンプルコードの実際の実装について解説を行う。
モデルのインスタンス
model = FNO(
in_channels=cfg.arch.fno.in_channels,
out_channels=cfg.arch.decoder.out_features,
decoder_layers=cfg.arch.decoder.layers,
decoder_layer_size=cfg.arch.decoder.layer_size,
dimension=cfg.arch.fno.dimension,
latent_channels=cfg.arch.fno.latent_channels,
num_fno_layers=cfg.arch.fno.fno_layers,
num_fno_modes=cfg.arch.fno.fno_modes,
padding=cfg.arch.fno.padding,
).to(dist.device)
loss_fun = MSELoss(reduction="mean")
optimizer = Adam(model.parameters(), lr=cfg.scheduler.initial_lr)
scheduler = lr_scheduler.LambdaLR(
optimizer, lr_lambda=lambda step: cfg.scheduler.decay_rate**step
)上記でモデルのインスタンスと損失関数・最適化の設定を行っている。損失関数はMSEで定義されている。各種パラメータは後程説明をする。
データローダーの定義
norm_vars = cfg.normaliser
normaliser = {
"permeability": (norm_vars.permeability.mean, norm_vars.permeability.std_dev),
"darcy": (norm_vars.darcy.mean, norm_vars.darcy.std_dev),
}
dataloader = Darcy2D(
resolution=cfg.training.resolution,
batch_size=cfg.training.batch_size,
normaliser=normaliser,
)正規化の設定とデータローダーの設定を行っている。前述したとおり、ここでのデータは事前計算したものを読むのではなく、各イテレーションごとに計算をしている。
学習の実行
@StaticCaptureTraining(
model=model, optim=optimizer, logger=log, use_amp=False, use_graphs=False
)
def forward_train(invars, target):
pred = model(invars)
loss = loss_fun(pred, target)
return loss
@StaticCaptureEvaluateNoGrad(
model=model, logger=log, use_amp=False, use_graphs=False
)
def forward_eval(invars):
return model(invars)
if loaded_pseudo_epoch == 0:
log.success("Training started...")
else:
log.warning(f"Resuming training from pseudo epoch {loaded_pseudo_epoch + 1}.")
for pseudo_epoch in range(
max(1, loaded_pseudo_epoch + 1), cfg.training.max_pseudo_epochs + 1
):
# Wrap epoch in launch logger for console / MLFlow logs
with LaunchLogger(**log_args, epoch=pseudo_epoch) as logger:
for _, batch in zip(range(steps_per_pseudo_epoch), dataloader):
loss = forward_train(batch["permeability"], batch["darcy"])
logger.log_minibatch({"loss": loss.detach()})
logger.log_epoch({"Learning Rate": optimizer.param_groups[0]["lr"]})
# save checkpoint
if pseudo_epoch % cfg.training.rec_results_freq == 0:
save_checkpoint(**ckpt_args, epoch=pseudo_epoch)
# validation step
if pseudo_epoch % cfg.validation.validation_pseudo_epochs == 0:
with LaunchLogger("valid", epoch=pseudo_epoch) as logger:
total_loss = 0.0
for _, batch in zip(range(validation_iters), dataloader):
val_loss = validator.compare(
batch["permeability"],
batch["darcy"],
forward_eval(batch["permeability"]),
pseudo_epoch,
logger,
)
total_loss += val_loss
logger.log_epoch({"Validation error": total_loss / validation_iters})
# update learning rate
if pseudo_epoch % cfg.scheduler.decay_pseudo_epochs == 0:
scheduler.step()
save_checkpoint(**ckpt_args, epoch=cfg.training.max_pseudo_epochs)
log.success("Training completed *yay*")forward_train で学習中の予測部分を担っている。実際には、batch[“permeability”]を入力に、 出力とbatch[“darcy”]の誤差を返している。この時に、batch[“permeability”]の構造が、[バッチ, チャネル, 縦解像度, 横解像度]となっている必要がある。
評価をしながら、チェックポイントを保存するような構造になっている
各種パラメーターについて
ここでは、実装の時に必要となる各種パラメータについて説明をする。
config.yaml というファイルに設定項目がまとめられているので、順に解説をする。赤字はハイパーパラメーターで調整可能な変数である。
① decorder
デコーダーは高次元特徴量空間から出力の特徴量空間へと移す役割がある。
- out_features: 出力の次元。 サンプルでは $u(x)$ の次元なので 1 にする。
- layers: MLPの層数。増やせば増やすほどパラメータが増え表現力が大きくなる
- layer_size: 各層におけるニューロンの数。増やせば増やすほどパラメータが増え表現力が大きくなる
②fno
Fourier Neural Operator のこと
- in_channels: 入力の特徴量次元。 サンプルでは $a(x)$ の次元なので、1にする。
- dimension: 関数の定義域の次元。サンプルでは $x$ の次元なので、2にする。
- latent_channels: 中間状態の特徴量次元。増やせば増やすほどパラメータが増え表現力が大きくなる
- fno_layers: Fourier Neural Operatorの層数。増やせば増やすほどパラメータが増え表現力が大きくなる
- fno_modes: フーリエ変換後に採用するモードの数。増せば高周波の特徴も捉えられる。
- padding: 境界付近の高速フーリエ変換を安定化させるための0埋めする個数
他は、モデルの設定ではなく、最適化やデータ生成等の設定なので、省略する。
まとめ
今回は、Fourier Neural Operator のサンプルコードの解説をした。
要点は以下のとおりである。
- Fourier Neural Operator は入力・出力ともに構造格子からなるデータが必要である。
- CNNとは違い、全てのデータで解像度を固定する必要はない。
Fourier Neural OperatorはCNNベースに比べて柔軟な設計が可能である一方、離散化が構造格子に限るという点は、欠点として存在する。
これを克服するモデルとして、Geometoric Informed Neural Operator 1(GINO) というものが存在する。
GINOはGNNとFNOを融合した手法で、任意離散に対応したモデルである。解説記事を今しばらくお待ちいただきたい。
- Fourier Neural Operator と同じ著者であり、おそらく博士課程(FNO は修士課程?)の時に創出したようだ。天才である。 ↩︎

コメント