この記事でわかること
- Fourier Neural Operatorがどのようなことをしているか、イメージできる
- Neural Operator や Fourier Neural Operatorの強みを理解できる
対象読者
- 機械学習による物理シミュレーションの高速化に取り組んでいる人・興味がある人
- CAE従事者で、計算時間や解析の設定難易度に課題を感じている人
- Fourier Neural Operator によってCAE解析を高速化したい人
- Fourier Neural Operator を理解したい人
はじめに
Fourier Neural Operatorは、偏微分方程式の計算を機械学習によって高速化する手法の一種であるNeural Operatorに含まれる手法である。
PhysicsNeMoにも、採用されている手法でもあり、Neural Operator系統の手法でもっとも有名な手法ではないか。
その特徴はメッシュフリーな手法なことで、学習データに無いようなメッシュの切り方でも精度良く予測することができる。(図3参照)
Fourier Neural Operatorがどのようなことをしているからザックリでもいいから理解すること
まずNeural Operatorの簡単な説明をしてから、Fourier Neural Operatorの説明をする。
詳細は原論文を参照すること。
Neural Operatorについて
概要
従来の機械学習では、
\begin{equation} f:\mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\label{eq:nn} \end{equation}
と有限次元のユークリッド空間の間の写像しか表現できなかった。
これでは、偏微分方程式の近似解を求めるときに、空間解像度(=離散点数)が同一の学習データでなければならない。 ()
これを解消する一つのモデル1が、Neural Operatorである。詳細は論文を確認してほしい。ここでは簡単に概要を説明する。
Operatorとは、演算子のことをいい、関数空間から関数空間への写像のことである。つまり、次のように定式化できる。
\begin{equation} \mathcal{K}:f \mapsto g\label{eq:no} \end{equation}
例えば、積分や微分など、関数に作用させて、関数が得られるような操作のことである。
Neural Operatorの場合は、$f, g$ は有限次元のユークリッド空間の間の写像である。
偏微分方程式の文脈でいうと、例えば、初期条件 $u(x, 0)$ から解 $u(x, t)$ を求める手法が、(近似的な)解演算子である。
()を克服する手法の中で、Neural Operatorの特徴は、写像を出力することにある。
つまり、定義域の任意の点 $x$ に関して、解 $u(x)$ を求められる。多くの手法では、メッシュなどの決められた離散点でしか解を得ることができず、メッシュの切り方によって精度が変化してしまう。
具体的な定式化
式(\ref{eq:no})のよくある定式化を一つ説明しよう。
入力となる関数を $f:D\rightarrow \mathbb{R}^{d_f}$ とする。ここで、$D\subset \mathbb{R}^{n}$ の有界開集合であり、通常は(時)空間である。
出力となる関数を $g:D\rightarrow \mathbb{R}^{d_g}$ とする。
通常、入力 $f$ はPDEの初期条件や境界条件、非定常解析の場合は、ひとつ前の時刻の系の状態である。
出力 $g$ は求めたい状態である。
この時、式(\ref{eq:no})の具体的な表現は次のようになる。
\begin{equation} g(y) = \mathcal{K}(f(x)) = \int_D \kappa_\theta(x, y)f(x) dx\label{eq:no2}\end{equation}
$\kappa_\theta$ が学習可能パラメータ $\theta$ を持つ学習可能関数で、多くの場合、式(\ref{eq:no2})を繰り返し作用させ、解 $g(y)$ を得る。
式(\ref{eq:no2})を実際に使うときは、$D$ を離散化する必要があるが、式(\ref{eq:no2})の計算量は離散点数 $n$ に対し、$O(n^2)$ となるので、 複雑な形状の場合は、計算困難な場合が多い。
積分範囲を制限することで回避できる2が、長距離作用をとらえられなくなったり、解像度に依存するという欠点がある。
その欠点を克服したモデルがFourier Neural Operatorである。
- 式(\ref{eq:no2})について、$\int_D \kappa_\theta(x, y, f(x))f(x) dx$のように、学習可能関数の入力に$f(x)$を入れる場合もある。
- 式(\ref{eq:no2})について、$\int_D \kappa_\theta(x-y)f(x) dx$のように、学習可能関数の入力に相対位置を入れる場合もある。
- この定式化では、物理パラメーター(密度など)を入力にすることができない。物理パラメーター$c$を入力にするには、\begin{equation}\notag \int_D \kappa_\theta(x, y|c)f(x) dx\end{equation}と条件付けすればよい。
Fourier Neural Operator について
手法概要
前述のとおり、式(\ref{eq:no2})は計算量が困難である。
Fourier Neural Operatorでは、空間的に積分範囲を制限するのではなく、周波数領域で積分範囲を制限することで、その課題を解決している。
図1のように、入力関数 $f(x)$ (図1では $v(x)$ )に、フーリエ変換 $\mathcal{F}$ を作用させ、周波数空間で、式(\ref{eq:no2})の計算を実行し、逆フーリエ変換 $\mathcal{F}^{-1}$ を作用させることで、元の時空間次元での状態を復元している。
フーリエ変換を実施する際に、高周波成分を打ち切ることで計算量を削減している。
Fourier Neural Operator の特徴は、積分近似を空間領域ではなく、周波数領域の高周波成分を打ち切ることにより実施し、解像度に依存せず、予測を高速・高精度化していることにある。
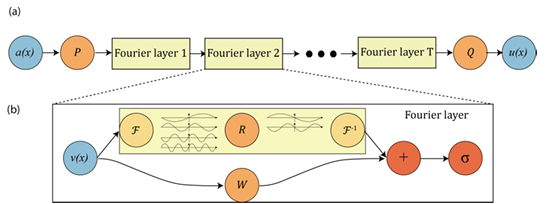
Fourier Neural Operator のイメージ図 (引用先:Firure2)
実際には、より多くの工夫を施しているが、詳細は別記事で述べる。
ここでいう周波数領域は、時間方向に対する振動成分とは限らない。領域 $D$ を周波数領域に変換している。$D$は、時空間であったから、周波数というのは時空間に対する振動成分である。
数値検証
原論文では、1次元Burgers方程式, 2次元Darcy流れ, 2次元Navier–Stokes方程式で検証をしているが、ここでは、1次元Burgers方程式を例に説明をする。
問題設定
1次元Burgers方程式は、下記のように書ける。
\begin{equation}\frac{\partial u}{\partial t} +u \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2}\label{eq:burgers} \end{equation}
ここで、$u$ は流速, $\nu$ は粘度である。
ここで、機械学習の予測タスクを、ある初速度 $u(0, x)$ に対し、式(\ref{eq:burgers})を満たす$u(1, x)$を求めることと設定する。この時、訓練データとテストデータで $\nu$ は同一とする。
つまり、式(\ref{eq:no})における $f$ が $u(0, x)$ で、$g$ が $u(1, x)$ である。
推論結果
実際の推論結果を図2で示す。
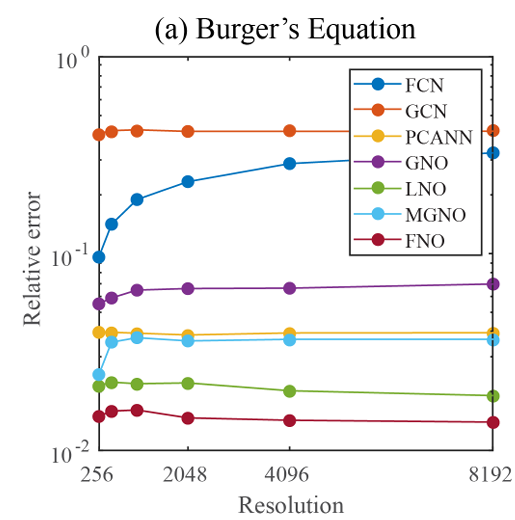
Burgers方程式の推論結果 (引用先:Firure3)
図2は横軸が解像度で、縦軸が精度を表す。
他手法については末尾にOがついている手法は、Neural Operator系列で、Nがついている系列はCNNやGNNなどの畳み込み系統の手法である。
図2を見ると、Fourier Neural Operatorが最も良い精度になっており、前述したとおり、解像度によらない学習が可能になっている。
超解像について
Fourier Neural Operatorは解像度によらず学習・推論ができるのなら、学習時の解像度と推論時の解像度が異なっていても推論できるのではないか?という疑問が自然と湧いてくる。
特に、低解像度の結果から高解像度の結果を予測できれば、学習データ生成の時間短縮やより高精度な推論につながると考えられる。一般に、低解像度の結果から高解像度の結果を復元する手法を超解像という。
論文中では超解像の検証として、2次元Navier–Stokes方程式で、低解像度のみで学習したモデルを使って、高解像度を予測した。
その結果が図3である
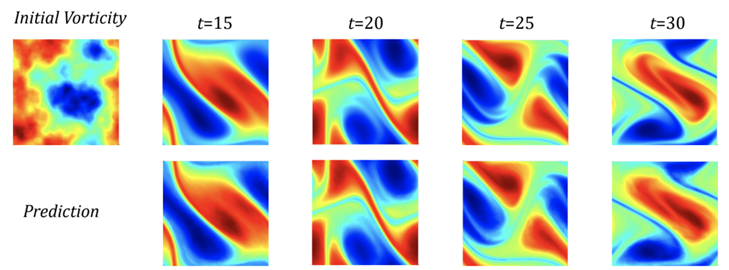
超解像の結果 (引用先:Firure1)
図3から、高解像度の結果をうまく推論できている3ことがわかる。
まとめ
今回は、Fourier Neural Operator について簡単に解説した。
要点は以下のとおりである。
- Fourier Neural Operatorは関数空間から関数空間を出力するNeural Operatorの一種である。
- Fourier Neural Operatorは、周波数領域で積分することによって、Neural Operatorの欠点である計算量を克服したモデルである。
- Fourier Neural Operatorは、解像度によらない推論が可能なので、超解像ができる。
- Fourier Neural Operatorは、同解像度でも、他手法よりも精度が高いモデルである
今回は、Fourier Neural Operatorの概要のみを解説した。特に、Fourier Neural Operatorのデメリットは解説できなかった。Fourier Neural Operatorは構造格子でなければ、計算量がそこまで優位にならないという欠点がある。別記事で、数式を交えながらFourier Neural Operatorの詳細を解説したいと思う。


コメント